Math

Algorithm Theory

算法导论

Optimal binary tree

In the range(i,j), if pick i as the root, then the left subtree will become (i,i-1) so have the dummy leaf di-1, so if pick j as the root, the right subtree become (j,j+1) have the dummy leaf dj.

Category theory

A category consists of objects and arrows that go between them.

1
2

-- A function can never be called
absurd :: Void -> a

Basic

Primitive : No property Abstraction Composition

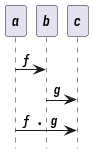
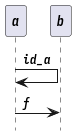
Identity f . id_a = f id_a . f = f

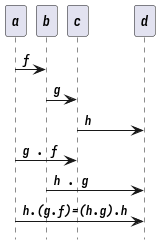
Associativity h . (g . f) = (h . g) . f

Function : A mapping of values to values

Set

Type are sets. In Set, objects are sets and morphisms (arrows) are functions. A set of morphisms between two objects in any category is called a hom-set.

_|_(Buttom)

Unicode ⊥. This “value” corresponds to a non-terminating computation.

1

f :: Bool -> Bool

Functions that may return bottom are called partial, as opposed to total functions, which return valid results for every possible argument.

Order

preorder partial order A set of morphisms from object a to object b in a category C is called a hom-set and is written as C(a, b) (or, sometimes, HomC(a, b)). So every hom-set in a preorder is either empty or a singleton.

Monoid

mappend maps an element of a monoid set to a function acting on that set A monoid is a single object category.

Category

[2017-05-09 Tue 23:17] Kleisli category a category based on a monad. any category C we can define the opposite category Cop just by reversing all the arrows. terminal object is the initial object in the opposite category.

Product

A product of two objects a and b is the object c equipped with two projections such that for any other object c’ equipped with two projections there is a unique morphism m from c’ to c that factorizes those projections.

Asymmetry

surjective + injective = bijection (isomorphism)

Kleisli category

Bifunctors

C x D = E

Covariant and Contravariant Functors

1
2

class Contravariant f where
contramap :: (b -> a) -> (f a -> f b)

Profunctors

C ^ op x D = E

Initial Object

The initial object is the object that has one and only one morphism going to any object in the category.

Yoneda lemma

CPS higher order function to data type [C,Set] (C(a,-),F) =~ Fa

Represetable

c(L1,-) = Rc Data type as the key to get value

Lambda Mathematics

Definitions

Zero: λs.(λz.z) 1 ≡ λsz.s(z) 2 ≡ λsz.s(s(z)) 3 ≡ λsz.s(s(s(z))) S ≡ λwyx.y(wyx)

Multiplication (λxyz.x(yz))

Conditionals T ≡ λxy.x F ≡ λxy.y ∧ ≡ λxy.xy(λuv.v) ≡ λxy.xyF ∨ ≡ λxy.x(λuv.u)y ≡ λxy.xTy ¬ ≡ λx.x(λuv.v)(λab.a) ≡ λx.xFT

conditional test Z ≡ λx.xF¬F (zero predicate)

Linear algebra

Linear transformation

Associative Use new base to represent the old A . B = C use column of A vector to represent the basis in B